Master Thesis: Reinforcement Learning for Optimizing Compute Clusters

Main Contributions
- Generalization of Q-learning to multi-objective environments
- Implementation of a proof-of-concept on synthetic examples
- Dashboard visualization of performance over time
Preview
Abstract
Hyperparameter tuning of complex systems is a problem that relies on many decision-making algorithms and hand-crafted heuristics. Developers are often called upon to tune these hyperparameters by hand using their best judgment. But over time, systems experience a natural drift and configurations become obsolete. The maintenance of such systems is expensive, does not scale well, and calls for what is known as autonomic computing — the ability of networks to tune themselves without outside intervention.
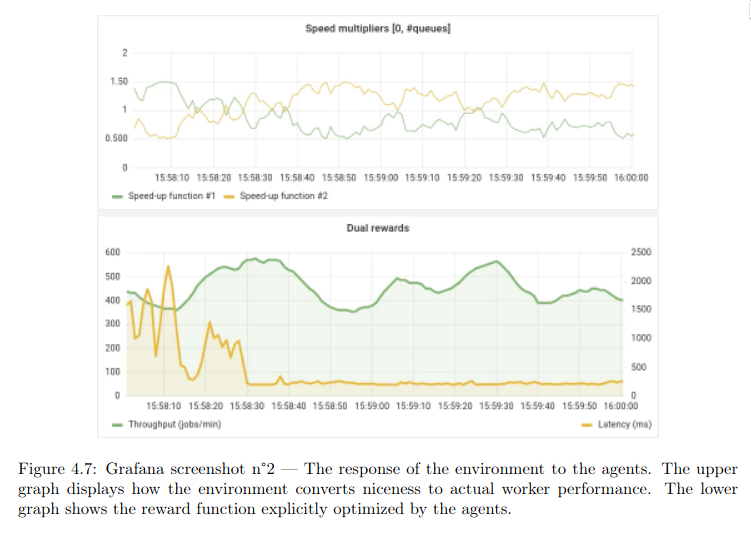
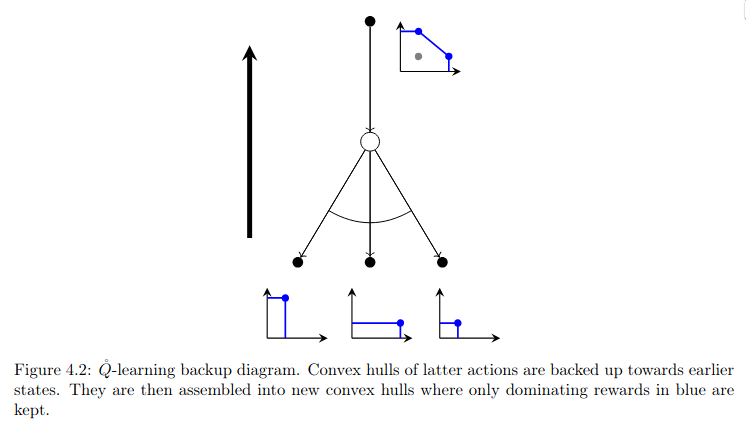
In this thesis, we explore the use of reinforcement learning (RL) as an autonomic computing solution for complex systems. We use reinforcement learning as a zeroth-order optimizer for systems abstracted as black boxes. Implementing RL agents is a two-step process that comprises tuning the underlying model and training the agent on the task. When properly executed, the RL agents are capable of successfully enhancing a wide range of heuristics and even creating new ones from scratch. Moreover, we show that decision tree approximators can be used on top of Q-learning to handle large state spaces or improve the ability of agents to generalize from unknown samples. Several adjustments were made to usual RL training algorithms to accommodate for decision tree ensembles in an online learning setting. The latter part of the thesis sets out to build a faithful simulation for streaming processing, an instance of a complex system. The simulation follows sound concurrency principles and decouples the environment from the agent by using a message-passing library. Once in the simulation, the pipelines are optimized by a series of agents subject this time to a multi-objective reward function. Throughput and latency are chosen as the competing metrics to optimize for. Using this formulation, we introduce the multi-dimensional equivalent of Q-learning, namely ◦Q-learning. After which we study the behavior of agents in the dynamic environment and rank them according to their performance. Agents are shown to converge quickly, adapt to the environment drift, and are robust to outside disturbances.




